Man stelle sich vor, die Welt bestünde aus kleinen und großen Dingen. Weiter sind diese Dinge sich in ihrer Form und in ihrem Wirken teils ähnlich, teils verschieden. So gelangen wir zu dem, was wir unsere materielle Welt nennen, in der wir leben. Unter der Form versteht man die einfachen Geometrieobjekte: 1.) die Punkte, 2.) die Linien, welche von Punkten aufgespannt werden, 3.) Flächen, welche durch Linien begrenzt werden und 4.) die Körper, welche durch ihre Seitenflächen begrenzt werden. Das Wirken von Dingen wird durch vielerlei Aspekte beschrieben - so auch von der Form. Ein rundes Objekt wird rollend leichter bewegt als ein Würfel und wird sich auch gleichmäßiger verhalten als jener. Doch wenn man genauer betrachtet, woher diese Unterschiede rühren, so erlangt man erstaunliche Erkenntnisse!
So sehen wir den Würfel als Körper. Doch dieser Körper ist, wie bereits festgestellt wurde, am Ende nur ein Gebilde aus Punkten. Beide Dinge sind demnach eher ähnlich als verschieden, da sie einen gemeinsamen Ursprung haben. Dass ein Würfel ungleichmäßig rollt liegt an seiner Anordnung der Punkte. Sie formen Kanten, die der Kugel scheinbar fehlen. Rollt man einen Würfel, so bleibt er am Ende auf einer Fläche liegen und selten auf der Kante selbst. Die Kugel rollt damit über ihre konvex-gebogene Fläche. Was wäre jedoch, wenn wir den Würfel auf die selbe Position der Kugel bringen und beide genau gleich rollen. Es würde sich nichts an dem Szenario ändern. Denken wir uns nun einen Körper, der aus zwei Würfeln besteht und rollen ihn abermals. Was wird passieren? Das Objekt würde wieder schneller zum Stehen kommen als die Kugel aber es stünde nicht mehr auf seinen Flächen, sondern nur noch auf den Kanten. Treiben wir dieses Spiel fort und erhöhen die Anzahl der ineinander verschachtelten und zueinander versetzten Würfel so wird daraus ein Objekt, das von der Ferne betrachtet keine eckigen Würfelflächen mehr besitzt und nur noch auf seinen Kanten stehen wird. Wir können gleichermaßen erkennen, dass es einer runden Form zustrebt. Erhöhen wir die Würfelzahlen um eine kaum fassbare Zahl ins das schier Unendliche, dann erhalten wir tatsächlich eine Kugel bzw. ein Objekt, das aussieht wie eine Kugel und genau so rollt. Wir haben somit gedanklich einen Körper in den anderen überführen können. Die Eigenschaft des Rollens diente hierbei als Beispiel.
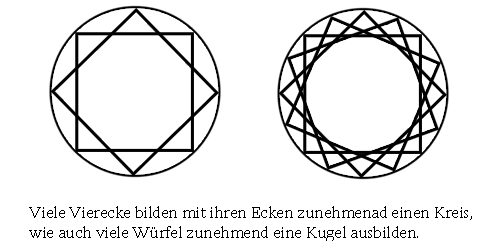
er Leser mag sich fragen: Wo ist nun der Bezug zur Proportionalität? Als proportional bezeichnen wir jene Prozesse, welche zu gleichmäßigen Wechselbeziehungen führen. Schütten wir einen Eimer Wasser in ein großes Becken, so hebt sich die dortige Wasseroberfläche. Die Entleerung des Wassereimers entspricht auch einer Senkung seines eigenen Wasserspiegels. Erhöht sich der eine Wasserstand, wird der andere erniedrigt. Dabei hebt und senkt es sich selten im selben Maße. Der Inhalt eines kleinen Eimers wird ein großes Becken nur zu einem kleinen Teil auffüllen können. Die Wirkung des Eimerinhalts auf den Inhalt des Beckens ist damit nicht gleich groß aber dennoch proportional, da sie immer den selben Effekt zeigt. Nehmen wir nun einen Eimer, der doppelt so groß ist, so wird sich dessen Auffülleffekt verdoppeln. Die Eimergröße ist damit sowohl proportional zu dessen Inhalt wie auch dieser Inhalt proportional ist zur Auffüllung. Dieses Gedankenexperiment lässt auch Rückschlüsse auf das vorangegangene mit Würfeln und Kugeln zu. Die Anzahl der zueinander verdrehten aber ineinander verschachtelten Würfel ist proportional zu der Anzahl der Kanten des Körpers. Je mehr Kanten der Körper hat, desto eher gleicht der der Kugelgestalt, das heißt seine Rollfähigkeit ist proportional zur Kanten- und Würfelzahl.
Entfernen wir uns nun von der Welt gleichgroßer Körper. Alternativ zu der Kantenzahl können wir auch z.B. die Körpergrößen variieren. Wenn wir einen Steinquader betrachten, wie sie häufig in Steinbrüchen geschlagen und zum Bau von Häusern verwendet werden, so beobachten wir Folgendes: Je größer der Quader ist, desto schwerer ist er auch. Dies ist nicht verwunderlich, denn fast immer sind die großen Dinge schwerer als die kleinen. Doch seine Größe ist wiederum abhängig von der Länge seiner Kanten, d.h. der Anzahl der Punkte, die aus denen Körper und Kanten aufgebaut werden. Verlängern wir den Block nur in eine Richtung bis er zu einem Balken wird, dann hat dieser Balken ein größeres Gewicht. Sein Gewicht ist in dem Falle proportional zur Länge einer Seite. Verlängern wir auch die zweite Seite tritt ein ähnlicher Effekt auf, gleiches bei der dritten. Das heißt, dass das Gewicht unseres Steinquaders jeweils proportional zu seinen drei möglichen Kantenlängen der drei Verschiebungsrichtungen ist: Westen-Osten, Norden-Süden, oben-unten. Doch kann man sie nur getrennt betrachten? Schneiden wir beispielsweise eine Scheibe längeren Quaderendes ab und steht diese Scheibe senkrecht auf eine der oben genannten Richtungen, so haben wir dennoch drei wirksame Proportionaltäten: jene aller drei Richtungen. Die entfernte Scheibe hat sowohl eine große Schnittfläche als auch eine Dicke. Trotzdem wird nur eine Länge verringert, denn die Schnittfläche bleibt gleich, egal wie dick die Scheibe ist. Das Quadergewicht wird durch die Variation einer Länge variiert und verhält sich somit proportional dazu: konstante Fläche mal variabler Länge ist gleich dem variablen Gewicht. Was hindert uns aber daran, den Steinquader nicht auch in den anderen beiden Richtungen zu verkürzen oder zu verlängern? Somit erhalten wir: variable Länge mal variabler Länge mal variabler Länge ist gleich dem variablen Gewicht. Wir haben somit die Proportionalität unserer Fläche in Bezug auf ihre Kantenlängen mit jener des Gewichts in Bezug auf die dritte Kante zusammengelegt. Es liegt daher nahe, dass auch andere Wechselbeziehungen in ähnlichem Maße verschachtelt ineinander spielen und durch Austauschen der Proportionalitätsfaktoren vereinfacht werden können. Die Fläche war nur ein Ausdruck ihrer Kantenlängen. Die physische Zerstörungskraft eines solchen Objektes müsste demnach auch dessen Längen beschreibbar sein, obgleich es noch geworfen/beschleunigt und dieser Prozess von jemanden oder etwas vorgenommen wird. Man kann somit komplexe Dinge mit Einheitsmaßen ausdrücken, wie beispielsweise mit einer Einheitslänge. Die Bestimmung der Proportionalität zwischen diesem einfachen Maß und dem komplexen Vorgang bleibt dabei in seiner Berechnung vorerst kaum fassbar und erfordert zunehmend experimenteller Wahrheitsfindung.
Ließen sich somit viel komplexere Zusammenhänge erklären wie das Wirken von alchimistischen Tinkturen und Arzneien? Allgemein bekannt ist, sie wirken je nach verwendeter/eingenommener Menge recht unterschiedlich. Mal ist etwas mehr besser, mal verschlechtert es das Ganze. Diese Beobachtung lässt sich auch in anderen Bereichen des Alltags machen: Sei es die Bewässerung von Pflanzen, welche gedeihen oder modern mögen oder der Genuss von saftigem Fleische, der so manchem wahre Gaumenfreuden aber auch so große Bauchschmerzen bereitet hat. Bei der Erforschung dieser Dinge stößt die einfach geometrische Betrachtung der Formen an ihre Grenzen und es mag Ziel zukünftiger Arbeiten sein, der absoluten Wahrheit der materiellen Welt ein Stück näher zu kommen.



